| |
|
|
COMPLEXITY SCIENCE
Differentiation, Centrality and Changes of State
In this section we connect the behavior of virtual discrete systems more directly to the study of social systems. The behavior or state of a social system, we argue, parallels the four states discovered for virtual systems, that is, there are only four states of such behavior: two types of order, chaos and complexity.
As in virtual discrete systems, these states can be recognized very often by direct observation of social behavior. For example, it is fairly easy to distinguish ordered behavior, as in a military parade, from the social chaos caused by an earthquake. In addition to direct observation, we may identify the state by the effect of a small local change. If the system is chaotic such a change will permeate and change the entire system, although staying within defined limits analogous to a strange attractor. In an ordered system, on the other hand, a small change will have only a local effect. For the complex state the effect of a local change depends on where it is introduced, but there will always be some constant internal structures which remain unchanged.
In the sociology literature many theorists have considered the states of social behavior, especially its degree of unity or solidarity. Such states represent the behavior of the social system over time, what we will call the social focus. Most of these studies consider only two types of output, as shown in Table 1, analogous to repetitive and fixed ordered states.
| Theorist |
Social Systems |
| Repetitive Ordered |
Fixed Ordered |
| Durkheim |
Organic solidarity in modern society |
Mechanical solidarity in traditional society |
| Tönnies |
Gesellschaft in organizations |
Gemeinschaft in communities |
| Weber |
Rule-based unity in organizations |
Common beliefs in religious sects |
| Redfield |
Heterogeneous unity in urban societies |
Homogeneous unity in folk societies |
| Hawley |
Symbiotic integration in corporate units |
Commensal relationships in categoric units |
| Table 1: Types of Social Systems |
The important question are: what causes changes in the state of social systems? What does order, chaos and complexity depend upon? We will use two variables from the social sciences to develop a relationship which has a great impact on the social state of focus. The first variable is differentiation, characterizing the internal organization of the system, related to Ross Ashby's variable of internal variety and the structure of the system itself (Ashby, R. 1966). The second variable is centrality, the impact of the new information on a system, labeled by Ashby as the variety of incoming information, both from the environment and from within the system itself.
We now examine in more detail the two variables of differentiation and centrality.
Differentiation
Increased differentiation, that is increasing the variety controlled by the structure of the system itself, keeps the system more focused and more predictable, according to Ashby. Differentiation can be related to Page's four parameters of diversity, connectedness, interdependence and adaptivity among individuals in the system, as discussed below (Page, 2009) [more info]. This interaction among individuals helps the system respond to its environment. As these four parameters increase their effect upon each other, differentiation increases so that the system becomes more predictable and its state tends toward order. While the state of the system is related to the values of these four parameters, it also depends upon centrality which we introduce after the following discussion of the four parameters.
Diversity
Diversity is the variety among the individuals that make up the discrete system. In social systems, diversity may be thought of as the different values or abilities of the individuals in the system. According to Durkheim and others, organizations become more unified and ordered because of increases in the variety of individual members to control the effects change. each specialized individual is trained to handle a specific problem so that the output remains focused. all other factors remaining constant, rising diversity increases differentiation which, in turn, leads to more ordered states. of course, this assumes that the specialized parts are integrated into an internal structure so that their own behavior is predictable.
In a virtual system such as a simple Cellular Automaton (CA) this is the variety of values that a cell in the system may assume. For the simple CA this is either one or two (black or white) but in other CAs this may be any range of numbers. In our recent paper Hay and Flynn, Changing the state of abstract discrete systems 19(3) (2011), we showed that in another type of CA structure called a Global Cellular Automata Network (GCAN)—that allowed us to hold all other parameters constant—increasing diversity caused increased order, just as Durkheim theorized.
Connectedness
The study of networks has grown rapidly in the past twenty years. A network consists of nodes and edges, where nodes are things, and edges are connections or relationships. Two of the descriptors used in the discussion of networks are degree—the number of connections at a given node—and path length—the minimum number of edges between any two nodes. The averages of these two parameters is sometimes used to describe networks.
In a random network, each node is connected randomly to other nodes. In such a network, small changes, such as adding a node or new information, usually permeate the network rapidly. Hence, such a network tends to be chaotic, that is, sensitive to change. Whether or not it is chaotic depends on the other three parameters as well but it does predispose the system toward chaos.
Stuart Kauffman in his studies of NK networks, which are random networks, found that with K = 2—two connections per node—the system exhibited order. Above K = 5 all systems were chaotic. In between K = 2 and 5 the state of the system varied between complexity, what he called the "edge of chaos", and chaos, depending on the rule structure, that is the interdependence (see next section) between the individual cells. So most of his random networks, but not all, yielded chaos.
Stephen Wolfram's studies were generally done on structured networks such as CAs where the edges of the network are most often between each cell (node) and its nearest neighbor. However, going from a one dimensional, two nearest neighbors, to a two dimensional CA with four or eight nearest neighbors results in a larger percentage of rules that produce chaotic states. Again, it appears that increasing the number of connections tends to move the system toward chaos.
However, there are two other important kinds of networks that are present in social systems but not directly reproducible in simple virtual discrete systems such as CAs. The first is the so called "small worlds network" and it is the social network we are all most familiar with (Watts, D., 1999, 2003). In a small worlds network each individual belongs to his or her group, clique, or cluster in which everyone knows everyone else. Individuals also have acquaintances outside of their cluster, known as weak connections (Granovetter, 1973). Such a system is characterized by high average degree and low average path length.
Since everyone is closely connected in the cluster the cluster tends toward chaos. Whether a cluster becomes chaotic also depends on the variety of information it is receiving from outside the system (centrality) but since there is a low variety of such information from weak connections, the cluster may not become chaotic but the possibility exists. Thus we can think of the small worlds network as tending to be on the "edge of chaos" or complex.
Another type of network is the so-called "scale free" network (Newman, 2006, pp335). An example is the internet, which is made up of hubs, sites, and connected sites. A scale-free network is a network whose degree distribution follows a power law, at least asymptotically. That is, the fraction P(k) of nodes in the network having k connections to other nodes ranges from a few with a large k number of connections to many with a few or low k, where for large values of k, P(k) ~ k^-y where y is a constant whose value is typically in the range 2<y<3, although occasionally it may lie outside these bounds.
Such networks are stable or robust in the face of most change and represent order because of size and the many sites. However, they are strategically weak because the loss of a very large site has a major effect. They can be considered analogous to repetitive order type 2.
There are many other networks that can be structured. Many of them have been utilized in studies of social science and in graph theory. They include inline, hierarchy, circle and star or hub networks. All of these are low degree networks, with few connections, and so are predisposed toward order.
The potential effect of different network structures on the state of a discrete system has been illustrated in our paper Hay and Flynn, The effect of network structure on individual behavior Complex Systems, Vol. 23 No. 4, Pg. 295.
Thus, while different types of networks can be expected to predispose the system toward a given state, the actual state realized depends upon the other three Page parameters, together with the effects of centrality. Hence, the relationship of connectedness to differentiation and, hence, the state of the system is complicated, and less easily summarized than for the other three page parameters.
Interdependence
Interdependence is how the relationship among individuals in the system is affected by the relative values and powers possessed by each individual. In CAs this interdependence is conveyed within the rules that govern how each cell decides how to change, based on the values of those cells to which they are connected. Thus the rule describes interdependence for the individual cells in the system.
In a social system, one individual may directly affect change in the values of others and are themselves similarly affected through these connections. We would expect chaos to be more likely at low interdependence because then each individual has more power to act independently On the other hand, where individuals within the system have high interdependence we would expect the system to tend toward order since the parts are more tightly interlocked with less likelihood of change. In general, then, high differentiation is related to high interdependence, and the greater liklihood of keeping the system in the ordered state.
The actual effect of interdependence is again dependent on the other three parameters. For example, interdependence is intimately tied to the network structure but in the general case and in real social networks the effect of each of these neighbors in the network on a given individual need not be the same and is related to the relative power of the individuals. The extreme example is a dictator who has high dominance over dependent citizens who may not have much interdependence over each other. This system will have extreme order, at least in the short term. In general, however, increasing the average interdependence of all the individuals leads to order.
Adaptability
Adaptability is the ability to change as a result of experience, including contacts with other individuals and incoming information (See the discussion of centrality below). Adaptability is a property of the individuals in the system but the effects of this property together with the other three parameters are seen as the adaptability of the system itself to its environment.
The unique feature of complex social systems is that they have the ability to adapt locally with the result that the overall system has adaptability. Other non-complex systems may be diverse, be connected in a network, and be interdependent, and even be programmed to respond to a known range of conditions—an automobile for example—but they do not have the ability to adapt to truly new conditions. They are not complex.
In virtual discrete systems, such as CAs, the behavior is determined by the rules, since they define the change that will occur in the value of a particular cell as a result of the values of its connected cells. There are many ways that such systems may be set up and the number of rules varies greatly from the 256 rules for simple CAs to billions of rules for more complicated virtual discrete systems. These rules establish how local change must take place. The rule essentially specifies what happens to an individual cell as a result of interdependence. In simpler virtual systems these rules are usually constant over time—although mutations may be introduced—and so they would not be seen as adaptable. There are, however, more complicated virtual systems such as Global Cellular Automaton Networks (Hay and Flynn, 2011) [more info] where the individual CA selects its own rule depending upon the behavior of its neighbors. This is adaptability.
In social systems there are 'instantaneous rules' which may be created in response to the situation, that affect the impact on an individual's values as a result of contacts with others. People may adapt their values and their interdependence very easily or only in the face of massive change. The parameter of adaptability itself may change with time but at any instant it can be viewed as the 'rule' at that instant. Again, the impact of these 'rules' is also dependent on the effect of the other three parameters, as well as the impact of centrality.
In summary, however, with the other parameters constant, as adaptability increases, that is, as the system becomes better at changing to control the impact of centrality, differentiation increases, and the system is more likely to remain in an ordered state.
Differentiation, then, is the result of the interaction of these four parameters, namely diversity, connectedness, interdependence, and adaptability. Differentiation increases with increasing diversity, interdependence, and adaptability. The effects of connectedness depends not only on the number of connections—where increasing those connections tends to raise differentiation—but also on the peculiar character of each connecting network, and so not easily generalized to a single measure. These four parameters interact in complicated ways, but, in general, increased differentiation results in increasing order.
Centrality
Centrality is a sociological concept with a lengthy history of development that has resulted in some differences in its meaning. Here we mean the flow of new and varied information into the system under study. Systems with high centrality receive a highly varied flow of information, some from within the system itself but most across its boundary from the surrounding environment.
To measure the flow of outside information, centrality requires that we properly define the system and its environment. The definition of the boundary of a system, as we defined it earlier, means that there is more interaction among individual parts than there is across the boundary.
As well, so that we can identify the source of the new information, we need to distinguish among system levels. Once we define a certain level as the system, then the parts become subsystems and the larger entity in which it is embedded is the suprasystems. If a corporation is chosen as the system, then the various departments are subsystems and its contractors, dealers, and the general public are the suprasystem. Of course, there are many levels, so that the departmental subsystem may be broken down into subsubsystems made up of individuals, and the suprasystem may consist of customers contained within a large suprasuprasystem of the general public.
Centrality for a business enterprise, then, is the variety of information presented to the corporation—the system—and includes sales and market information, economic forecasts, government actions and policies, competitor behavior and so on from the suprasystem as well as new ideas from subsystems.
The individuals within the system all react in some way to this information. They interact depending on their diverse backgrounds, position in the network, interdependence, and adaptability, which together make up the differentiation of the system that, in turn, reflects how the corporation responds to all this centrality. How this differentiation responds (adapts) to changes in centrality, thus influences the state of the corporation. In general, however, we can say that the higher the centrality, the more likely is the system to become chaotic since the higher the centrality, the less likely is it that the systems' differentiation can cope with the overwhelming impact of the new information.
In virtual discrete systems we can observe this effect even in simple CAs. For example, for a certain rule, with the same diversity (allowable values), connectedness, and interdependence we are more likely to push the system into a state of chaos if we increase the variety of the initial condition that represents centrality. In the example below, Figure 1, changing the initial condition from a single black cell—low variety—to a random set of black and white cells—high variety—changes the state of the system from order to chaos.
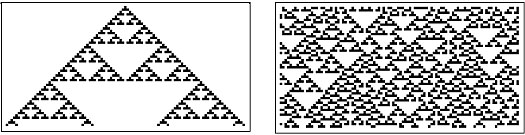 |
| Figure 11: These are two Cellular Automaton drawings of the so called rule 22 which governs interdependence and adaptability and with identical connections (nearest neighbors), diversity (values of either 0 or 1). In 12a centrality is introduced at only the beginning as a single black cell. In 12b centrality is introduced only at the beginning but it is a random series of ones and zeros. 12a is order type2 or repetitive order. 12b is chaotic. (Mathematica®) |
The Combined Effect of Centrality and Differentiation: d/c
 |
 |
| Figure 12: Phase diagram of the states of a social system as a function of differentiation (d) and centrality (c) |
|
The state of a system, its behavior over time, is primarily dependent upon differentiation and centrality. This may be a complicated relationship but at present we use changes in the ratio d/c to predict changes in the state of the system, that is, order is ditrectly proportional to differentiation and inversely related to centrality. Often one doesn't know the absolute values of d or c but when one or both are changing, their relative values can help predict the possibility of a change of state within a complex system. that is, when differentiation changes to become much higher than centrality, order is more likely, and similarily for the converse. A phase diagram of the relationship between the states of a system and the measures of differentiation and centrality is shown in Figure 2.
The relationship of system states to d/c can be illustrated in virtual discrete systems that are somewhat more complicated than those discussed here, as presented in our recent paper (Hay and Flynn, 2011) [more info].
The ability to predict this change of state by observing trends in differentiation and centrality and even being able to change states by changing these variables would be of great assistance in understanding and perhaps in managing social systems such as a business enterprise.
|
|

