|
COMPLEXITY SCIENCE
The Four States of Virtual Discrete Systems
The properties of discrete systems such as social systems can be inferred from studies of virtual discrete systems. Virtual discrete systems are usually studied on a computer and such systems are made up of individual cells that interact with each other in simple or in complicated ways and as a result of this interaction may change their behavior. We observe the behavior of virtual systems over time and these observations, we will argue, yield insights into the behavior of social systems.
To define a system, we need to establish the boundary. For social systems the boundary encloses those individuals who interact more with each other than with those external to the boundary.
The same definition of boundary can also be used to identify a particular virtual discrete system. In such a system we state precisely the alternative behaviors (values) permitted for each individual cell; the connections between the individuals; the effects that the behavior of connected cells has on each individual cell; and the amount and type of change that results. The virtual discrete system under study is the ensemble of all possible combinations of these relationships that are permitted by that system. As we will see below in all such ensembles some of these relationships produce a state of complex behavior and in this state are capable of emergence. Therefore they are all complex systems as defined in Complex Systems and System States.
Many such virtual discrete systems have been studied extensively by many investigators. There are hundreds of such systems, ranging from simple, to complicated structures, to systems based on numbers, to two and three dimensions, but by way of illustration let us examine cellular automata (CAs), the most widely studied of these systems. If we google cellular automata, we get about 754,000 results – click here for [more info] or here [more info]. Most of the information at these two sites is only indirectly connected to the discussion that follows. We base our work primarily on the work of Stephen Wolfram [more info]. A complete discussion of this material may be found in his book A New Kind of Science [more info], from which the references above are taken. CAs can be very complicated but our points may be made using the simplest CA structure.
A simple CA begins with a single row of cells each of which can take only one of two values, say 0 or 1, or, for illustration on a computer monitor, two colors, black or white. We begin by assigning a color to each cell in this first row, the “initial conditions”. For example, in a simple system we could make all the cells in the first row white with the exception of one black cell in the centre of this row.
We then establish a set of rules to determine whether a given cell will change its color or remain the same at the next time step. For our simple CA the color of each cell may change depending upon its color and the color of its two neighboring cells. There can be many rules for this change but a specific rule might be “if I am white and my neighbor on the right and my neighbor on the left are both black then on the next time step I must be black”. All cells do such an evaluation and then all take on the assigned color simultaneously to form the second row at time step 1.
 |
 |
| Figure 1: Simple Cellular Automaton beginning with one black cell (built with mathematica©) |
|
Figure 1 shows how this occurs for a given rule set beginning with one black cell at the centre of a row and all the other cells in the row white. For such simple CAs there are eight rules in each rule set to cover all the possible arrangement of the two colors of the three cells (2^3). Since all the cells can be rearranged there are in all 256 (2^8) possible sets of the eight rules for systems of 2 colors and three cells. For more complicated CAs with, for example, three colors instead of two the number of rule sets increases very rapidly to 7,625,597,484,987. (This can be reduced to 2187 by using so called totalistic rules. Click here for [more info]. For a description of totalistic CAs, click here for [more info].
A sample of the first 32 of the 256 rules is shown in Figure 2.
Figure 2: The first 32 of the 256 rule sets over 50 time steps for simple cellular automata
All of these 256 rule sets, which Wolfram has numbered from 0 to 255, generate output patterns which fall into only four classes or states of behavior: order (two types), chaos or complexity. Examples of these output patterns produced by simple CAs representing these four states are shown in Figures 3, 4, 5 and 6, identified by the rule set used to generate them.
 |
 |
 |
| Figure 3: Order type 1 state (Rule 4) |
|
Figure 5: Chaos state (Rule 30) |
 |
|
 |
| Figure 4: Order type 2 state (Rule 90) |
|
Figure 6: Complex state (Rule 110) |
These four states not only classify the four possible states of the 256 simple CAs but, it turns out, essentially all virtual discrete systems fall into one of these four states. This amazing discovery was established by Stephen Wolfram in the mid 1980s and is detailed in his book.
He has studied many additional CAs with many colors, different neighbors in two and three dimensions. These have many more rule sets than the simple CA. He has also examined a very large number of other virtual discrete systems with widely different structures and rules where, for example, the cells take their time steps individually, the lattice structure is not used, or the changing ‘colors’ are continuous functions. In total, he studied billions of virtual discrete systems, and essentially all exist in one of the four states.
The essence of this work is that each type of discrete system has within it all four states, or classes 1, 2, 3, 4 as he called them, and only these states. One can think of these states in the same way that we think of the states of matter as solid, liquid, and gas. They are similar in that by observation we can usually tell one state from another but there are significant other differences. For example, we can study the effect of a small change, say of one cell, to detect which state is present.
The essential point in what follows is that the evidence is overwhelming from Wolfram’s study of virtual systems that since real social systems are discrete systems they also exist only in one of these four states even though their interactions can be very complicated.
The Properties of the Four States
Order
There are two states of order, type 1 and type 2 as shown in figures 3 and 4. Order type 1 is focused and never changes. Order type 2 is repetitive. It may cycle through a number of different patterns but returns to the original pattern and begins the cycle again.
By looking at the history over a sufficient number of time steps we can usually identify order. We can also observe the effect of a small change in initial conditions and for a system in the ordered state the effect will remain local.
Although much of the mathematics and laws in the physical sciences refer to systems which are ordered, in fact, many real systems are actually either chaotic or complex.
Chaos
Chaos theory is a well defined area of science and the word chaos has a well-defined meaning that is distinct from common usage. The following is a brief review. For those wishing more information and much more detail including many of the important references, see [more info].
Poincaré first recognized chaos at the end of the 19th century but it wasn’t until the mid 70s that it began to be widely studied, even though the seminal work of Lorenz was first published in 1963. It has found far-reaching application in essentially all branches of science, for example, in fluid flow, irregular heartbeats, earthquake frequency, electrical circuits and encryption of messages. It has also been used in literary analysis, psychiatry and the visual arts.
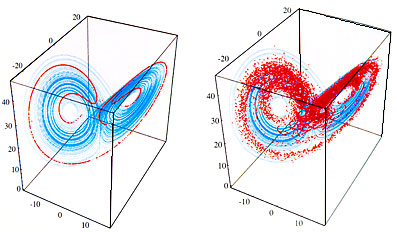
The modern study of chaos began with Lorenz’s 1963 paper. He was studying a model of a weather cell, that is, a cell with warm air rising in the centre and cold air falling outside. He described his model with three variables X, Y, Z that measured this flow. Note they are not the spatial dimensions x, y, z. He plotted the behavior of these three variables over time. Under many circumstances this plot looked like Figure 7. In chaos theory this is a example of what is called a strange attractor, and changes in the three variables are confined to this shape over time. Although they may have very different shapes, strange attractors are characteristic of chaos.
Lorenz also found that the slightest change in the value of a variable resulted in very large differences in outcome. This is ‘sensitivity to initial conditions’ (SIC) and is the defining characteristic of chaos. Figure 8 is another view of Lorenz’s strange attractor but plots the behavior of values for a group of slightly different initial conditions that start from almost the same small point on the attractor. In 15 time steps they have gone to very different parts of the attractor demonstrating sensitivity to initial conditions, SIC.
 |
 |
Figure 8: Divergence of trajectories. The blue is the Lorenz attractor. Starting from essentially one point in the three dimensional phase space, 10,000 trajectories, based on 10,000 slightly different initial conditions, are shown after T = 9 steps (the red lines on the left) and T = 15 steps (the red lines on the right). After 15 time steps the various trajectories have diverged enough to cover more than 1/2 of the attractor (From Strogatz 1994) |
|
Virtual discrete systems in the chaotic state can often be characterized by examining their pattern as shown in Figure 5 for a simple CA. However, as noted above, they are also characterized by a sensitivity to initial conditions. Figure 9 shows how the change of a single cell in one row eventually permeates the whole of a chaotic CA, unlike ordered systems where such changes remain localized.
 |
 |
| Figure 9: Rule 128, chaotic system, showing the effect of changing a single white cell to black partway through the development. (Original cells are grey; changed cells are black) [more info]. (Mathematica®) |
|
Most of the science we are familiar with, whether on a very large scale such as the solar system or very small scale such as quantum theory deals with linear systems, that is systems in which the effect is proportional to the cause. But many of the real systems we deal with everyday whether driving in traffic or interacting with other people are not linear. In these systems small causes may have very large effects. They are called non-linear systems and chaos occurs only in such systems. As Steven Strogatz has said “non linearity is the puppeteer of chaos” (Strogatz, Chaos, The Teaching Company).
Although the behavior is complicated, it is not random, as all values remain on the strange attractor. Further studies have shown that there is often a distinct reproducible route to chaos for a certain large group of systems (quadratic systems). This route is very precise and can be described by universal relationships.
In general, chaotic systems often appear to be randomly generated. They are not. They are deterministic and the next step value depends entirely on the current value. In contrast, in random systems the next step is dependent on probabilities. Furthermore, very simple deterministic systems may be chaotic. For example the CA in Figure 5 is a very simple system and the same exact chaotic outcome is repeated each time we run it.
This is a very rudimentary discussion of chaos and there is a large literature available. The book Chaos: Making a New Science by James Gleick is an excellent starting point.
For our purposes, a chaotic discrete system may appear random but it is deterministic and, most importantly, is sensitive to initial conditions, that is, a very small change can have a very large effect.
Complexity
 |
 |
| Figure 10: A complex system, showing interacting structures after beginning with random initial conditions (rule110) (Plotted with Mathematica®) |
|
A small percentage of the rules of a particular virtual discrete system generate complexity as illustrated in Figure 6. The complex nature of this CA is better revealed if, rather than starting from a single black cell, we begin with a random distribution of black and white cells. Figure 10 shows such a system using the same rule as figure 5. Here we see structures moving down the system through each time step. Some intersect and form new structures and some remain unchanged. This is a mixture of order and chaos, and is characteristic of the complexity state.
In such systems, the effect of a small change depends on its location. In some cases it will permeate the entire system. but some of the ribbon like patterns will still remain. In other situations, the effect will remain local and the ribbon like patterns will be unaffected.
Stephen Wolfram also found that the rules which generate complex states, such as the simple rule 110 in Figure 10 can be programmed to emulate any other discrete system. Hence, it is a universal system. Other CAs can also be programmed to be universal but they become extremely complicated, for example requiring each cell to take on 17 or 19 colors, but the simple rule 110 produces the complex state and is universal. For our purposes virtual discrete systems in the complex state are where such creativity takes place and we would expect this to be similar in discrete social systems. It is in this state that emergence takes place.
Kauffman’s NK Virtual Discrete Systems and The Four States
Another example of a virtual discrete system which produces the four states is Kaufmann’s NK systems.
Stuart Kauffman has studied a particular discrete system called a Boolean NK network in great detail (Kaufmann 1992). A Boolean network consists of N sites each of which can be thought of as a light that can be on or off. Each site is randomly connected to K other sites. Whether a site is off or on is determined by the values of the K sites connected to it. Each site utilizes a randomly selected Boolean rule, such as, “if the value of each of the K connected sites is on at a certain step then it will turn off at the next step”. Such a Boolean rule can be quite long as K gets larger. All N sites make this evaluation at the same time using their randomly selected Boolean rule. In this manner the dynamics of the system are observed through time. We could also think of this system as N pixels or cells on a computer each of which can be either black or white.
For sufficiently large Ns and K = 2 Kauffman observed ordered behavior, that is, large fixed islands that remained either on or off over time and changed, if at all, very slowly. For K ≥ 5 he observed chaotic behavior, lights constantly changing with no particular pattern, and very sensitive to small changes.
For certain systems and particularly by biasing the selection of the Boolean rule so that more cells are more likely to select rules that, for example, turn them on, he was able to arrive at what he called the edge of chaos. At the edge of chaos we have a mix of order—fixed islands—together with the constantly changing lights of chaos. This is similar to the complex state described by Stephen Wolfram as class 4.
Stuart Kauffman was primarily interested in biology and evolutionary biology and he studied the ability of these NK systems to adapt and evolve under mutation to “higher fitness”. For example, in the space of all possible genotypes each genotype can be assigned a “fitness”. Depending upon the distribution of fitness, such a genotype “landscape” can be more or less mountainous, where the height of each genotype is its fitness. A population of individuals beginning from different points in the landscape then moves via mutations across the landscape. Selection is the result of different reproduction rates depending upon fitness. Depending upon the detailed structure, the population may arrive at various fitness peaks or move about the landscape (Kaufmann, 1993, p33). He found that “systems lying in this interface region between order and chaos, the edge of chaos, may be those best able to adapt and evolve”. There is also evidence that NK systems tend to evolve towards the edge of chaos (Kaufmann, 1993, p218).
It is in the complex state, Wolfram’s class 4 and Kaufmann’s edge of chaos that creativity and change, emergence, can take place.
In summary, in all the billions of virtual discrete systems studied by Wolfram and others, only four states were found and all four were found in each of the different kinds of systems. It seems safe to assume that even though social systems seem more complicated than those constructed on a computer, they too will end up either in one of the two states of order, or the chaotic state, or the complexity state.
|

